2020-01-06 Excel 2019
fogalmak
Csak érdekességként mesélem el, hogy az Excel legfeljebb tizenöt karakter hosszú számokkal tud aritmetikai műveletet végezni, ezért az ennél hosszabb számok utolsó karaktereit a szám egész részében nullára cseréli illetve a szám tört részében elhagyja. Ezt a jelenséget adatbevitelkor is megfigyelhetjük.

És ha még nem untuk meg a kísérletezést, adjuk össze ezt a két tizenöt-karakteres számot: 444 444 444 444 444, 777 777 777 777 777. Az eredmény 1 222 222 222 222 220. Ha ez pénz, és a mienk, akkor üsse kő, lemondunk arról az egy Forintról!
Hasonló az eljárás amikor meghatározott „pontosággal” számolunk. Például, ha euróval dolgozunk elegendő a százados-pontosság, azaz a tizedes-elválasztótól jobbra két karakter, de az adóbevallást már ezres pontossággal kell elkészítünk, azaz a tizedes-elválasztótól balra a harmadik karakterig nullák állnak majd a végeredményben.

A pontosság kialakítása tehát a szám egész részében a „felesleges” karakterek nullára cserélésével illetve tört részében, elhagyásával történik. A pontosság neve annak a helynek az értéke a tízes számrendszerben, amelyen a pontosság szerinti utolsó karaktere áll. Ennek a szám-karakternek a beállítása történhet a törölt vagy nullára cserélt karakterek értékét figyelembe véve (kerekítés) vagy figyelmen kívül hagyva (csonkolás).
Ha a pontosság szerinti utolsó szám-karaktert egy négynél nagyobb szám követ, akkor a pontosság szerinti utolsó karaktert meg kell növelni eggyel. Ez a kerekítés alapszabálya, amit mindenki ismer. A kerekítés azonban egy szám többszörösére is történhet és akkor már más a szabály. Ott van például a vásárláskor alkalmazott ötre kerekítés. Ha az összeg utolsó szám-karaktere nulla vagy öt, akkor nincs módosítás, ha egy vagy kettő, akkor mi járunk jól, ha három vagy négy, akkor a bolt. Sőt lefelé és felfelé is kerekíthetünk. Ilyenkor az alapszabályt „kikapcsoljuk” és tekintet nélkül a felesleges szám-karakterek értékétől, csökkentjük illetve növeljük a kerekítendő számot. Ha elképzeljük a számegyenesen az eredeti-, majd a képzett számot, akkor balra vagy jobbra történő-, sőt nullához közelítő, vagy attól távolodó kerekítésről is beszélhetünk.
Ugye azt, mindnyájan tudjátok Gyerekek, hogy a látható és a tényleges cellatartalom nagyon gyakran nem azonos! És most nem a cellában álló képletre gondolok, hanem a számok kerekített megjelenítésére. A biztonság kedvéért, nézzünk erre is példát!
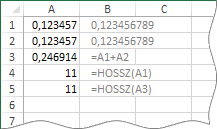
A képen látható A oszlop szélessége nyolc és fél karakter. Ezért a program az oszlop első két cellájában álló számot (0,123456789), valamint a harmadik cellájában lévő képlet eredményét (0,246913578) hat tizedesjegyre kerekítve jeleníti meg. Ha azonban megszámláltatjuk a konstansok illetve a képzett szám karaktereit (A4, A5), akkor már a cella valóságos tartalmáról kapunk információt.
CSONK
Csonkolásnak nevezzük azt az eljárást, amikor a pontosság szerinti karaktereket, az értéküktől függetlenül, a szám tört-részében elhagyjuk, illetve a szám egész-részében nullára cseréljük. Ezt a műveletet a kétargumentumos CSONK függvénnyel végeztethetjük el. Első kötelező argumentumával az átalakítandó számot deklaráljuk, a második, nem kötelezővel a „csonkolás” mértékét határozhatjuk meg. Utóbbi egy előjeles egész szám. Nézzünk néhány példát a függvény működésére! Az átalakítandó szám: 56 789,98765.

Tehát, [1] ha a második argumentum a negatív szám, akkor a nullára cserélendő karakterek számát határozza meg, a tizedes elválasztótól kezdődően, balra haladva, [2] ha hiányzik, akkor a tizedes elválasztótól jobbra eső összes karakter törölve lesz, [3] ha pozitív szám, akkor a megmaradó karakterek számát deklarálja a tizedes elválasztótól jobbra haladva. Ha a második argumentum tört szám, akkor azt a program egészre csonkolja.

INT
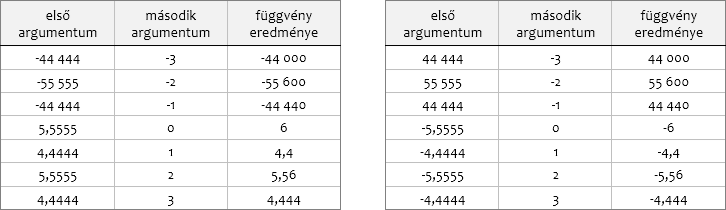
A függvény az egyetlen argumentumával meghatározott tizedes tört számot a számegyenesen balra, egészre kerekíti. A természetesen a kerekítést fogalmát most már matematikai, azaz kiterjesztett értelmében használom.
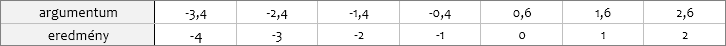
KEREKÍTÉS
A kétargumentumos függvény az első argumentumával deklarált számot, a második argumentumával meghatározott pontosságra kerekíti, a kerekítés alapszabálya szerint. Ha a második argumentum tört szám, akkor azt a program egészre csonkolja.
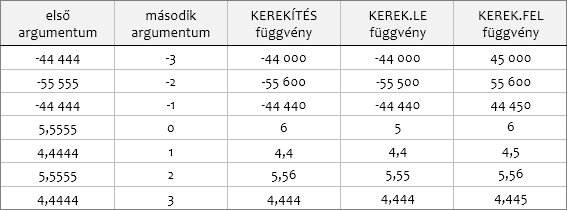
KEREK.LE - KEREK.FEL
A két függvény a KEREKÍTÉS-sel alkot egy családot. Argumentumaik azonosak. Az első argumentumukkal deklarált számot, a második argumentumukkal meghatározott pontosságra kerekítik, a nullához közelítve (KEREK.LE) illetve a nullától távolodva (KEREK.FEL). Ha a függvények második argumentuma tört szám, akkor azt a program egészre csonkolja.
TÖBBSZ.KEREKÍT
Kétargumentumos függvény. Az első argumentumával deklarált számot, a második argumentumával meghatározott szám többszörösére kerekíti. A függvény először elosztja az első argumentumát a második argumentumával, majd az egészre kerekített hányadost megszorozza a második argumentumával. Természetesen a két argumentum törtszám is lehet, de eltérő előjelük #SZÁM! hibaértéket generál.
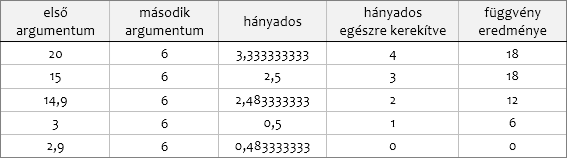
PADLÓ.MAT - PLAFON.MAT
A két függvény az első argumentumukkal deklarált számot a második argumentumukkal meghatározott szám többszörösére kerekítik. Mint a TÖBBSZ.KEREKÍT ők is a két argumentum hányadosát képzik, majd a hányadost a KEREK.LE és a KEREK.FEL függvényekkel egészre kerekítik. A függvények eredménye az egészre kerekített hányados és a második argumentum szorzata lesz.
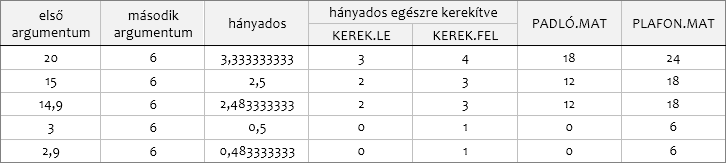
Természetesen az argumentumok tört számok is lehetnek. Ez a két függvény már kezelni tudja az eltérő előjelű argumentumokat is. A kerekített szám mindig az első argumentum előjelét örökli, függetlenül második argumentum előjelétől.
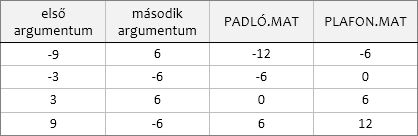
A példán nem csak az előbbi állítást ellenőrizhetjük, de megfigyelhetjük a függvények működését a számegyenes negatív tartományában is. A PADLÓ.MAT itt is a kisebb értékű többszöröst adja, azaz a nagyobb negatív számot, ahogy a PLAFON.MAT is a nagyobb értékű negatív többszöröst adja, azaz a kisebb negatív számot. Tehát elmondhatjuk, hogy a szám előjelétől függetlenül a kerekítést a PADLÓ.MAT a számegyenesen balra-, a PLAFON.MAT jobbra „mozdulva” végzi el.
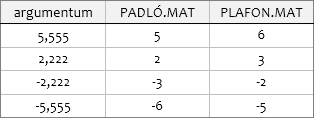
Ez a függvények szokásos működése, de harmadik, elhagyható argumentumukkal módosíthatjuk ezt a viselkedést! Ha az argumentum hiányzik vagy nulla (0), akkor a függvények a szokásos módon működnek, ha azonban egy (1), akkor már más „filozófiát” követnek: a PADLÓ.MAT a számegyenesen mindig a nullához közeledve, a PLAFON.MAT a nullától távolodva adja a legközelebbi többszöröst. Ez a módosított működés csak a negatív számok kerekítésekor ad eltérő eredményt.

De nem csak a harmadik, de a második argumentum is elhagyható. Ilyenkor a PADLÓ.MAT balra-, a PLAFON.MAT jobbra, egészre kerekíti az egyetlen argumentummal deklarált számot. Azaz PADLÓ.MAT( <szám> ) = KEREK.LE( <szám> ; 0) és PLAFON.MAT( <szám> ) = KEREK.FEL( <szám> ; 0).
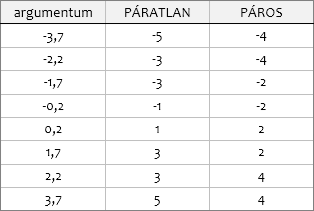
PÁRATLAN - PÁROS
A két függvény az egyetlen argumentumával deklarált számot a számegyenesen a nullától távolodva a legközelebbi páratlan- (PÁRATLAN), illetve páros (PÁROS), egész számra cseréli.

 margitfalvi.arpad@gmail.com
margitfalvi.arpad@gmail.com
