2020-10-14 Excel 2019
változó méretű tartomány összegzése
Van egy oszlopunk, legyen a felirata „bevétel”, és ennek celláiba jegyezzük fel a jövedelmeinket. Szeretném egy cellában, amely nem a bevétel oszlopban áll, folyamatosan követni ezeknek a pénzeknek az összegét! Tehát nem az utolsó szám után álló, folyamatosan mozgó összegről van szó! Az nem nagy ügy: adatbázis táblázat, összegsor. Hanem erről!
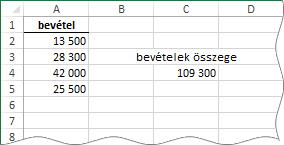
A probléma az, hogy a C4 cellában álló =SZUM( A2:A5 ) képletet újra és újra módosítanunk kellene, minden új bevétel rögzítését követően. A legegyszerűbb az, ha a SZUM függvénynek nem egy tartományt adunk meg, hanem a teljes „A” oszlopot: =SZUM( A:A ). Ez a megoldás elég általános, és más függvényeknél is alkalmazzák.
De a profik ezt sohasem így csinálják! A tényleges, csak a számokat tartalmazó cellákat adják meg. De, hogyan? A tartomány első cellája adott. A mi esetünkben ez az A2-es cella. Állapítsuk meg az utolsó számot tartalmazó cella sorszámát az oszlopban! Az nem jó kiindulás, mert előfordulhat az oszlopban más, az összeadandóktól független szám is! Inkább az első üreset keressük meg! Az a biztos! =HOL.VAN( IGAZ ; ÜRES( A:A ) ; 0 ). A HOL.VAN első argumentuma a keresett adat, a második az egyoszlopos vagy egysoros tartomány hivatkozása, a harmadik a keresés módját határozza meg. Az ÜRES függvény egy cellát vizsgál, üres-e. Logikai értéket ad eredményül: ha üres, akkor IGAZ, ha nem, akkor HAMIS. A HOL.VAN harmadik argumentumának nullája a pontos egyezéses keresést írja elő. Van még egy bibi! Nekünk nem egyetlen cellát kell megvizsgálni, hanem többet. Ez sem probléma! Tömbös kiértékelést kérünk a Shift + Ctrl + Enter billentyűparanccsal!

Tehát az „A” oszlop hatodik cellája az első üres cella. Ebből már képezni tudjuk az összeadandó számok tartománya utolsó cellájának hivatkozását: ”A” & HOL.VAN( IGAZ ; ÜRES( A:A ) ; 0 ) - 1. Természetesen ezt így nem írhatjuk be a képletbe, csak az INDIREKT függvénnyel, amely feldolgozza az argumentumában álló kifejezést és eredményül az összeállított cella-hivatkozást adja.

Ha a #HIÁNYZIK hibaértéket kaptuk eredményül, akkor valószínűleg elfelejtkeztünk a képlet Shift + Ctrl + Enter-es lezárásáról.
A változó méretű tartományok deklarálásának van egy másik, nagyon elterjedt módja: megszámláltatják a DARAB2 függvénnyel az oszlopban álló adatokat és ebből képzik a szám-tartomány utolsó cellája hivatkozását. Például, ”A” & DARAB2( A:A ). Ennek a módszernek két hibája van. Lefoglalja a teljes „A” oszlopot és feleslegesen néz át több mint egymillió cellát. De, hát a HOL.VAN( IGAZ ; ÜRES( A:A ) ; 0 ) kifejezéssel pontosan ugyanilyen felesleges munkát végeztetünk. Nem egészen! A HOL.VAN függvény első argumentumának első (!) előfordulását keresi. Tehát, ha megtalálta leáll az ellenőrzéssel.
minden n. szám összeadása
Ez egy nagyon gyakori probléma és nem csak összeadásnál kerül elő: egy táblázat minden meghatározott sorát akarom csak feldolgozni. Például, minden harmadik, vagy minden hetedik sorát. Matekosan megfogalmazva, minden n. sorát.
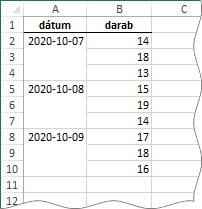
A képen egy konkrét feladatot látunk. Adjuk össze a dátumok minden harmadik darabszámát! A megoldáshoz a SOR függvényen keresztül vezet az út. Ennek a függvénynek vagy nincs argumentuma, vagy ha van, akkor az egyetlen cellahivatkozás illetve cellahivatkozást eredményező kifejezés. Az argumentum nélküli függvény annak a sornak a számát adja eredményül, amelyben áll. Az argumentumos pedig az argumentumával meghatározott hivatkozás sorának számát.
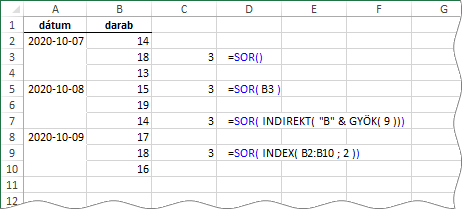
Hát ezzel, azért még nem jutottunk túl messzire! Kellene egy közös tulajdonságot találnunk ezekhez a sorszámokhoz: 4, 7, 10. A kulcs biztos, hogy a hármas, mert hogy minden harmadik számot kell összeadnunk. Igen! Ha elosztjuk a számokat hárommal akkor mindig egyet kapunk. A maradék-képzésnek van saját függvénye az Excelben. Nem fog nagy meglepetést okozni, ha elárulom, hogy MARADÉK a neve. És az sem, hogy két argumentuma az osztandó és az osztó.
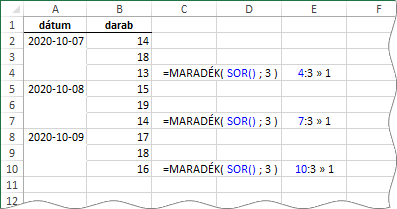
Most már csak ezeket a műveleteket kellene excelesen megfogalmazni: [1] vedd sorban a B2:B10 tartomány celláit, [2] nézd meg hogy a cella sorának száma egyet ad-e maradékul, ha elosztod hárommal, [3] ha igen, akkor a cellában álló számmal képezz összeget! Mivel több cella feldolgozásáról van szó egyetlen képletben, ezért biztos, hogy tömbös kiértékelést kell kérnünk és a HA függvény is kell majd a feltételes művelet miatt.

Természetesen a SOR függvény argumentumában megadott tartomány oszlopa közömbös. Megadhattuk volna az első oszlopot is, A2:A10. Az eredmény ugyanaz. A HA függvény tömbös kiértékelésű változatában csak a feltételt, illetve a feltételeket, valamint a vizsgálandó tartományt kell deklarálnunk.
rangsor egy szakaszának összegzése
A rangsor a számok torna-sora. Elől áll a legnagyobb szám és a sor végén a legkisebb. A számok rangsor-pozícióját egy sorszám, az index mutatja. Ha a rangsor egy szakaszáról beszélünk akkor a rangsorban egymás után álló számokról van szó. A rangsor-szakaszt az első és az utolsó számának indexe azonosítja. Ha egy rangsor-szakasz számait össze akarjuk adni, akkor a szakasz pozíciója határozza meg az eljárást.
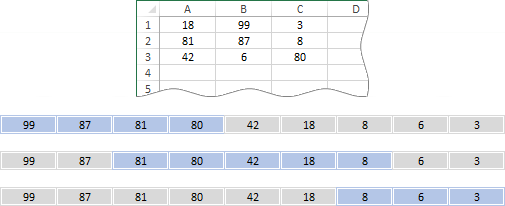
A kép tetején álló számok rangsorát látjuk három példányban. Az összegzendő szakaszokat kék színnel jelöltem. Fogalmazzuk meg a három feladatot! [1] Add össze a négy legnagyobb számot! [2] Add össze a rangsor legnagyobb számait, a harmadiktól a hetedikig! [3] Add össze a három legkisebb számot!
Az első két esetben a NAGY a harmadikban a KICSI függvényt kell használnunk, tömbös kiértékeléssel. A NAGY a rangsor elejéről a KICSI a végéről ad vissza számokat. A két függvény argumentumai azonosak: az elsővel a számok tartományát, a másodikkal a visszaadandó legnagyobb, illetve legkisebb számok indexének tömbjét deklaráljuk. Az eredményül kapott számokat a SZUM függvénnyel adjuk össze. Ha csak néhány indexet kell megadnunk akkor a képletben tömb-állandót használunk. Magyarul, beírjuk az összeadandó számok indexét az előírt formában. A képlet szerkesztését követően nem kell tömbös kiértékelés kérnünk, mert a tömb-állandót a program tömbösen dolgoza fel!

Néhány index beírása nem gond, de hosszabb szakaszok megadása már fáradságos lenne ezzel a módszerrel. Egy mesterfogást fogunk alkalmazni: a SOR függvénynek sorok tartományát határozzuk meg feldolgozásra. Például, {=SOR( 1:5 )}. Ez a képlet egy tömböt ad eredményül, amelynek elemei sorszámok. Az első az egyes, az utolsó az ötös. Természetesen ez az öt sor semmilyen logikai kapcsolatban sincs az összeadandó számokkal, se a rangsorukkal. Mivel a képletünk már nem tartalmaz tömb-állandót, ezért Shift + Ctrl + Enter billentyű-paranccsal kérnünk kell a tömbös kiértékelést.

Gyakori feladat számok meghatározott százalékú legnagyobb illetve legkisebb számainak feldolgozása. Páldául, adjuk össze az A1:C3 tartomány számainak legnagyobb huszonöt százalékát vagy a legkisebb ötven százalékát!
A megoldás logikáját már ismerjük, az egyetlen újdonság az összes szám darabszámának megállapítása. De ez sem okoz gondot, ott a DARAB függvény. A darabszámot szorozni kell a megadott (x) százalékkal és a szorzatot egészre kell kerekíteni, hiszen darab-számokról van szó. Íme így fest, meghatározott tartományban álló számok legnagyobb x százaléka összegének képzése!


 margitfalvi.arpad@gmail.com
margitfalvi.arpad@gmail.com
