2020-06-22 Excel 2019
Halmazok összetételének elemzéséről lesz szó. A következő kérdésekre keressük a választ. [1] Milyen elemek fordulnak elő egy adott halmazban? Vagy másként fogalmazva, melyek a halmaz egyedi elemei? [2] Hányszor fordulnak elő a halmazban az egyedi elemek? [3] Ha a halmaz intervallumának szakaszokra osztásával kategóriákat alakítunk ki, akkor az egyes kategóriákba, hány elemet sorolhatunk? [4] Melyik a domináns elem, vagy másként fogalmazva melyik elem fordul elő legtöbbször a halmazban? Az első, a második és a negyedik kérdés adattípus-független, de a harmadik csak számhalmazra vonatkozhat.
A második kérdésre egyszerű a válasz, ha ismerjük a DARATELI függvényt. Nézzünk egy példát! Az A2:A13 tartományban egykarakteres számok állnak. Hányszor fordulnak elő a számok a halmazban. Jelenlegi ismereteink szerint, két megoldás közül választhatunk: vagy közvetlenül az elemek mellé, vagy egy erre a célra készített lista elemei mellé írattatjuk ki az előfordulás-számokat.
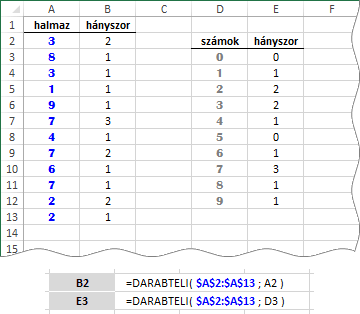
Egyik variáció sem tökéletes: az elsőben a halmaz ismétlődő elemei, a másodikban a halmazban nem szereplő számok rontják az áttekinthetőséget. Tehát készítenünk kell egy olyan listát, amelyben csak a halmazban előforduló számok szerepelnek! És ehhez tömbös feldolgozású képletre lesz szükségünk!
De még mielőtt összeállítanánk ezt a listát, állapítsuk meg a halmaz egyedi elemeinek számát. Haladjunk lépésenként!

Az első lépésben megszámláltattuk, hogy a halmaz elemei hányszor fordulnak elő a halmazban. Képletünk így kerül végrehajtásra: a program veszi az A2 cellában álló számot és megszámlálja hányszor fordul elő az A2:A13 tartományban. Ez az előfordulás-szám lesz az eredmény-tömb első eleme. Ezután veszi az A3 cellában álló számot és megszámlálja hányszor fordul elő az A2:A13 tartományban. Ez a darab-szám az eredmény-tömb második eleme. És így tovább.
Az eredmény-tömb egyesei a nem ismétlődő elemekhez tartoznak. Összeadva az egyeseket ötöt kapunk. Ehhez kellene még hozzáadni az ismétlődő elemek „egyeseit”. De azok nem egyesek… És akkor valaki, rájött, hogyan lehet az ismétlődő elemek előfordulás-számaiból is egyest csinálni. A reciprokjukkal. Az egyeseken nem változtat az osztás, mert egyben az egy, egyszer van meg, de ha az ismétlődő elemhez tartozó előfordulás-számok reciprokjait összeadjuk, akkor mindig egyet kapunk. Nézzük csak a példánkat!
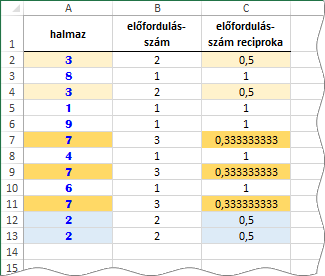
A két hármashoz tartozó előfordulás-szám reciprokok összege egy: 1/2 + 1/2. A három heteshez tartozó előfordulás-szám reciprokok összege szintén egy: 1/3 + 1/3 + 1/3. És így tovább. Tehát a második lépés egy mesterfogás, amire csak a kevesek jönnek rá maguktól, a többség ellesi egymástól.
És akkor jöjjön az egyedi elemek listája. Ez is egy mesterfogáson alapul, amit a tömbképlet létrehozásáról szóló cikkben mutattam be.

A feladat megoldásához vezető nagy ötlet a képlet másolásával bővülő tartomány volt, amelynek kiindulópontja mindig a leendő lista felett álló cella. A mi esetünkben a C2. Ezt a találmányt fogjuk alkalmazni az egyedi értékek listájának létrehozásakor is.
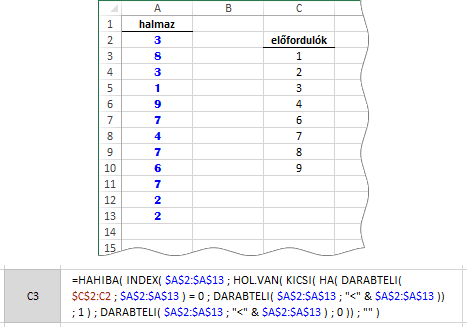
Hát igen! Ez a képlet így egyszerre, elég nagy falat. Lépésenként egyszerűbb lesz! Az áttekinthetőséget javítsuk a műveletek elnevezésével.

A negyedik lépésben a legkisebb szám kiválasztása szándékosan nem a MIN függvénnyel történik. A MIN függvény ugyanis logikai értékeket vizsgálva is számot ad eredményül, nullát vagy egyet, a KICSI viszont, ha nem talál számot, akkor a #SZÁM! hibaértéket. És pont erre van szükségünk a képlet másolásakor. Ha már nincs egyedi szám, akkor legyen hiba. A lista elkészítését követően a DARABTELI függvénnyel megállapíthatjuk az előfordulás-számokat.
Az első két kérdésre már válaszolni tudunk: milyen elemekből áll a halmaz és ezek az elemek hányszor fordulnak elő a halmazban. Most vegyünk egy másik példát, hogy a harmadik kérdésre is felelni tudjunk.
A lenti táblázat egy üzlet eladásait tartalmazza. Az eladások általában háromszáz- és hétszázezer forint közöttiek. Meg akarom állapítani a vásárlások összetételét százezer forintos intervallumokat használva. A tömbös feldolgozású és több eredményt adó GYAKORISÁG függvényt fogom alkalmazni.
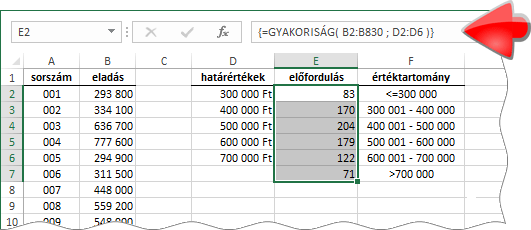
Ahogy látjuk a függvény két argumentuma egy-egy tartományt határoz meg. Az első az elemzendő halmazt-, a második az értéktartományok felső határértékeit tartalmazza. A halmaz-elemek kategorizálása a „melyik az a legkisebb szám a határértékek közül, amely nagyobb vagy egyenlő a vizsgált számnál” elv alapján történik. Ezért a határértékeket rendezetten, növekvő sorrendben kell megadnunk. A képlet-szerkesztés megkezdése előtt kijelölendő tartomány celláinak száma mindig eggyel több legyen, mint a felső határértékek celláinak száma. A képlet összeállítását a Shift+Ctrl+Enter billentyűparanccsal fejezzük be!
Visszatérve a példánkhoz, a 829 vásárlásból 83 esik az első kategóriába és 71 az utolsóba. A többi kategória már nagyobb elemszámú. A legnépesebb a harmadik, 204 vásárlással.
A számhalmaz intervallum-szakaszok szerinti összetételét ábrázoló oszlop-diagramot hisztogramnak nevezik. A hisztogram része egy vonaldiagram is, amely az elemszám göngyölített összegét mutatja, a teljes halmaz elemszámának százalékában.
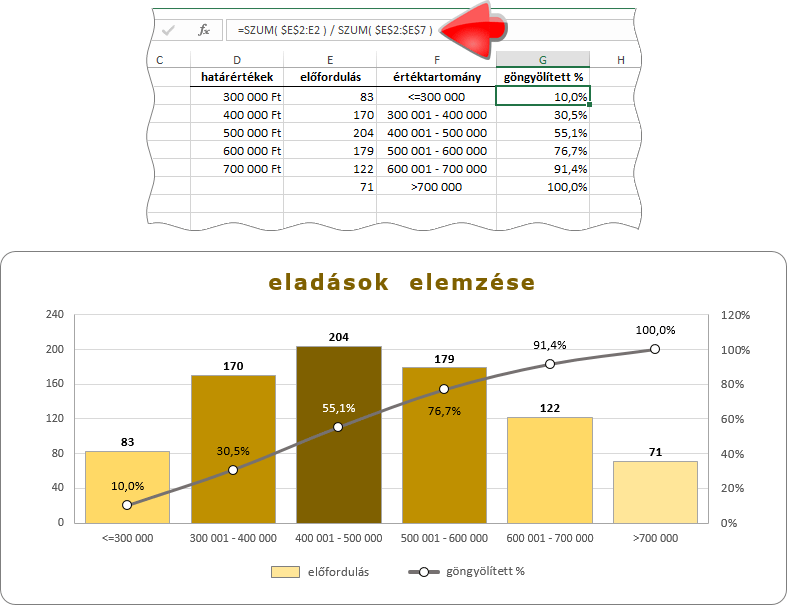
A program 2019-es változata két hisztogram-típust tud létrehozni. Az első, amelyet „Hisztogram”-nak nevez, nem tartalmaz vonaldiagramot, a második, amelynek „Pareto” a neve, már igen, de az viszont a kategóriákat, nem az intervallumuk szerint növekvő, hanem elemszámuk szerint csökkenő sorrendben jeleníti meg. Tehát balról jobbra haladva, először a 400 001-est (204 elem), azután az 500 001-est (179 elem), majd 300 001-est (170 elem)… Hogy miért Pareto? Azt csak a microsoftosok tudnák megmondani. Élt ugyan egy ilyen nevű olasz-francia tudós, Vilfried Pareto, de neki nem sok köze volt a matematikához.
Szóval aki, beépített hisztogramot vagy paretot akar, az az eladásokat (B2:B830), aki viszont hisztogram-klasszikot szeretne, az az előfordulás-számokat (E2:E7) és a göngyölített százalékokat (G2:G7) jelölje ki. Ezután a hisztogram-paretosok a Beszúrás, Diagramok, Statisztikai diagram beszúrása, a klasszikosok a Beszúrás, Diagramok, Az összes diagram megtekintése vezérlőt válasszák! Utóbbiak se járnak rosszul, mert a megnyíló parancstáblán a program az elképzelésünknek megfelelő, kombinált oszlop- és vonaldiagramot ajánlja fel, két értéktengellyel.
A szép diagramhoz és a jó munkához idő kell… Ha az nincs, akkor is kötelező: [1] a kategória-tengely feliratait utólag deklarálni (F2:F7) és [2] a két értéktengely osztásait szinkronizálni. Azaz az előfordulás tengely fő osztásait át kell állítani negyvenre.
Akkor már csak a leggyakrabban előforduló halmaz-elem kiválasztása van hátra, amit a statisztika módusznak nevez. Emlékszünk még a mediánra? A medián a rangsor közepén álló elem, a módusz meg ezek szerint a leggyakoribb. Mindkettővel van egy kis hiba. A páros elemszámú halmazban nincs a rangsorban középső pozíció, és a halmaz legnagyobb előfordulás-száma több elemre is vonatkozhat.
Na de foglalkozzunk most a leggyakoribb elem kiválasztásával. A program két függvényt kínál a művelet elvégzésére a MÓDUSZ.EGY-t és a MÓDUSZ.TÖBB-t. Argumentumaik lehetnek számok, számot eredményező képletek, cellák és tartományok. Ezek szerint a két függvény csak számhalmazok vizsgálatára alkalmas.
A MÓDUSZ.EGY azt a legmagasabb előfordulás-számmal rendelkező számot adja eredményül, amelynek első előfordulása megelőzi a többi, legmagasabb előfordulás-számú számot a képletben vagy a munkalapon, balról jobbra illetve felülről lefelé haladva. Magyarul, a függvény a legtöbbször előforduló számot adja eredményül, de ha több ilyen is van, akkor azt, amely először megjelenik a képletben, illetve a munkalapon.
A MÓDUSZ.TÖBB egy tömbös kiértékelésű, több eredményt adó függvény. A kijelölt cellákat feltölti a legmagasabb előfordulás-számú számokkal, illetve ha már nincs több ilyen, akkor a #HIÁNYZIK hibaértékkel. Nézzük meg mindezt a gyakorlatban.
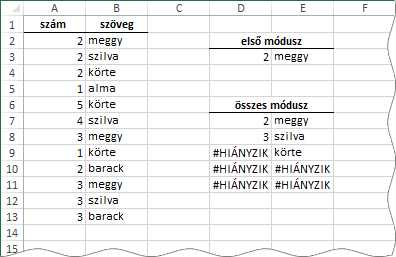
Az A2:A13 tartományban álló számok közül a kettes és a hármas fordul elő legtöbbször, négyszer-négyszer. A B2:B13 tartományban a meggy, a szilva és a körte a leggyakoribb, mindegyik háromszor szerepel.

Tehát szöveg-halamazok vizsgálatához is tudjuk használni a program módusz függvényeit, csak nem közvetve, hanem egy számokból álló tömb közbeiktatásával (Tessék, már megint egy mesterfogás.)

 margitfalvi.arpad@gmail.com
margitfalvi.arpad@gmail.com
