2019-10-24 Excel 2019
Ha egy szám-halmaz elemeit nagyság szerint sorrendbe állítjuk, úgy, hogy a legnagyobb szám álljon elől, akkor ez a halmaz elemeinek rangsora. Tessék csak nyugodtan úgy mondani Tanító bácsi, hogy torna-sora! Rendben, Pistike! Szóval, a rangsor a számok torna-sora. A halmaz egy elemének a rangsorban elfoglalt helyét, azaz rangsor-pozícióját, egy sorszámmal deklaráljuk.
A halmaz elemeinek számát a DARAB függvénnyel határozhatjuk meg. Ha a számok különbözőek, akkor az utolsó rangsor-pozíció azonos a halmaz elemeinek számával. A program rangsor-kezelő függvényeivel közvetlenül meghatározhatjuk [1] a halmaz legnagyobb illetve legkisebb számát vagy értékét, [2] a rangsor elején illetve a rangsor végén, meghatározott helyen álló számot, [3] a rangsor közepén álló számot és [4] a halmaz elemeinek rangsor-pozícióját.

A két MAX és a két MIN kötetlen argumentum-számú függvények. Természetesen ez nem végtelen számú argumentumot jelent, náluk is kettőszázötvenöt a határ. Az argumentumaik lehetnek konstansok, cella és tartomány hivatkozások és képletek. A MAX és a MIN függvények csak a számokat és a nem „hivatkozásként” megadott logikai értékeket vizsgálja. Az IGAZ értéke egy a HAMIS-é nulla.

A két függvény a szövegeket a logikai értékkel azonos módon kezeli: ha „hivatkozásban” áll akkor figyelmen kívül hagyja, de képlet-argumentumban kiértékelésre kerül és hibát okoz (#ÉRTÉK!). A MAXA-val és MIN2-vel már mindkét adattípust korlátozás nélkül vizsgálhatjuk. A szöveg értéke nulla. Az üres cellák a négy függvény eredményét nem befolyásolják.

Milyen bénaság ez, Tanító bácsi, hogy az egyik függvény-változatot A-val a másikat 2-sel jelölik? Én sejtem mi történhetett, Pistike! A jakutföldi Fegya, aki a MAXA-t programozta és a kalkuttai Rahul, aki a MIN2-t, valószínűleg nem tudhattak egymásról és redmondi Alex, akinek ellenőrizni kellett volna őket, gyengélkedett, mert elcsapta a gyomrát tegnap este fekete kaviárral.
Ha nem a teljes halmazt kívánjuk vizsgálni, akkor a MAXHA és a MINHA függvényeket használhatjuk. A függvényeknek azonos az argumentum listája.

A függvények első argumentuma tehát az a tartomány, ahol a legnagyobb illetve a legkisebb számot keresniük kell. További argumentumaik párban állnak. A párosok első eleme egy tartomány, amelynek celláiban a párosok második elemével deklarált feltételek teljesülését kell ellenőrizniük.
Az elemzendő tartománynak és a feltétel tartományoknak azonos méretűeknek és azonos tájolásúaknak kell lenniük. Az első három argumentum megadása kötelező. Az elemzendő tartomány üres és nem szám adattípusú elemei a függvények eredményét nem befolyásolják. A feltételek szintaktikája mindenben azonos a feltételes megszámlálás függvényeinek feltétel-argumentumaiban alkalmazandó szabályokkal.
A feltétel tartományok celláinak ellenőrzése sorrendben történik. Először a tartományok első celláit vizsgálják a függvények. Mindegyiket a saját feltételével. A következő munkamenetben a második-cellák kerülnek sorra, majd minden harmadik. És így tovább, egészen az utolsó cellákig. Ha az aktuálisan vizsgált cellák tartalma minden feltétel tartományban megfelelt a saját kritériumának, akkor az elemzendő tartomány azonos cellájában álló adat hozzáadódik a szűkített halmazhoz.
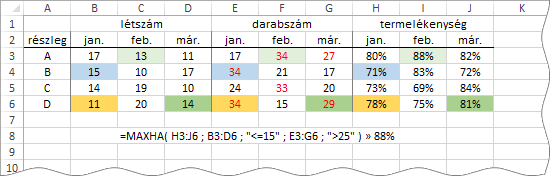
A fenti képen egy gyár termelési adatait látjuk. Arra voltunk kíváncsiak, hogy legfeljebb tizenötös létszám és legalább huszonhatos darabszám esetén mi volt a termelékenység legmagasabb értéke az első negyedévben.
A halmaz meghatározott sorszámú legnagyobb, illetve legkisebb elemét a kétargumentumos NAGY illetve KICSI függvényekkel választhatjuk ki. Például, a harmadik legnagyobbat vagy a második legkisebbet. Első argumentumukkal a halmazt tartalmazó tartományt deklaráljuk, a másodikkal pedig a kiíratandó elemet határozzuk meg a rangsor végpontjától kezdődő sorszámmal.

A képen látható munkalap hetedik sorában a képzeletbeli rangsor áll, a balról illetve a jobbról induló sorszámokkal. Előbbieket a NAGY, utóbbiakat a KICSI függvény használja.
A két függvényt általában nem egyetlen-, hanem meghatározott számú elem kiíratására használjuk. A következő képen erre a tipikus alkalmazásra látunk egy példát.
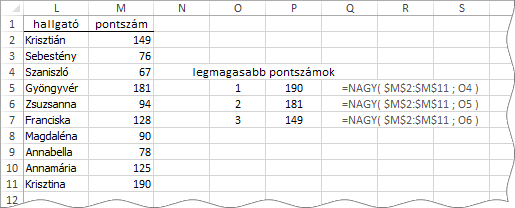
A függvény első argumentumának abszolút hivatkozása „rögzíti” az elemzendő tartományt a képlet másolásakor, míg a második argumentum relatív hivatkozása teszi lehetővé a sorszámok léptetését a másolatokban.
Szép, szép, Tanító bácsi! De az életben nem csak a legmagasabb pontszámokat akarjuk tudni, hanem azt is, hogy ki érte el őket! Így igaz Pistike! Ennek a feladatnak az elvégzésére az INDEX függvény szolgál... De használatát majd egy másik alkalommal mutatom be, most maradjunk a számok rangsoránál!
Ha valaki már hallott a mediánról, akkor biztos, hogy ezt hallotta: a középen álló szám. Meg azt, hogy: ugyan annyi van alatta, mint felette. Igen, a medián a rangsor közepén álló szám neve. Természetesen csak páratlan elem-számú halmaz esetén van ilyen pozíció. Ha nincs, akkor képezni kell egy nem valóságos-, egy ál-, egy pszeudó mediánt!
Az Excelben a rangsor közepén álló elemet a kötetlen argumentum-számú MEDIÁN függvénnyel választathatjuk ki. Argumentumai cella- és tartomány¬hivatkozások, konstansok és képletek lehetnek. A függvény eredményét az üres cellák, a szövegek és a logikai értékek nem befolyásolják. Páros elem-szám esetén a képzett medián a rangsor közepén álló két szám számtani közepe.

A képen az első sorban álló számok rangsora: 128, 3, 2. Középen a hármas áll, akkor ő lesz a három szám mediánja. Az ötödik sorban álló számok rangsora: 128, 3, 2, 0. A rangsor középen a hármas és a kettes áll. Akkor ennek a két számnak a számtani közepe lesz a négy szám mediánja: (2+3)/2 » 2,5.
A MEDIÁN-t általában határérték képzésére használjuk: meghatározzuk vele azt a számot vagy azt a dátumot, amellyel egy csoport, elemeinek egy számszerűsíthető tulajdonsága alapján, két azonos nagyságú részre osztható. Vegyünk egy egyszerű példát: egy cégnél év végén maradt egy kis szétosztható pénz, de ez csak a kollégák felének elegendő. A főnök leginkább a hűséget díjazza. A belépési dátumok alapján határozzuk meg, kik számíthatnak a plusz pénzecskére!
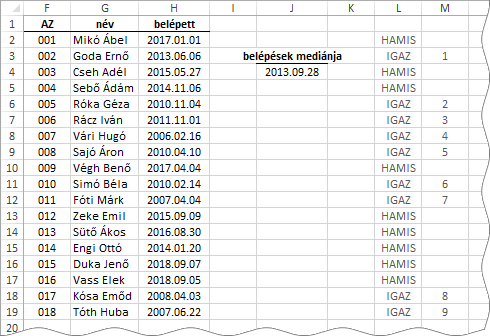
Ahogy az azonosítókból (AZ) látjuk tizennyolc dolgozója van a cégnek. Miután megállapítottuk a belépések mediánját, egyenként megvizsgáltuk a dátumokat, kisebbek-e a mediánnál (=H2<$j$4). Kilenc ilyen dátumot találtunk...
Az eddig ismertetett függvények egy meghatározott rangsor-pozícióban álló számot adnak eredményül. A RANG.EGY ezzel szemben a halmaz egy számának rangsor-pozícióját állapítja meg. Három argumentuma van: az elsővel a számot, a másodikkal a halmazt tartalmazó tartományt, a harmadik, elhagyható argumentummal a sorszámozás irányát deklaráljuk. A harmadik argumentum lehetséges értékei: [hiányzik vagy 0] a legnagyobb számtól-, [1] a legkisebb számtól kezdődik a sorszámozás.
A függvény csak számokkal dolgozik, az üres cellákat, a szövegeket és a logikai értékeket figyelmen kívül hagyja. Ha az első argumentumával meghatározott számot a függvény nem találja a halmazban a #HIÁNYZIK hibaértéket kapjuk eredményül.
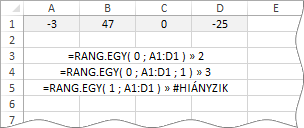
Az első sorban álló négy szám rangsora: 47, 0, -3, -25. A harmadik sor képletével a nulla rangsor-pozícióját kívántuk megállapítani. Az eredmény kettő lett. A negyedik sor képlete csak a függvény harmadik argumentumával bővült: egy. Ez a deklaráció a sorszámozás megfordítására utasította a függvényt. Ezért kaptunk eredményül hármat. Az utolsó sorban álló képlettel az egy rangsor-pozícióját kívántuk megállapítani, de mivel a függvény az egyest nem találta a számok között, a #HIÁNYZIK hibaértéket kaptuk eredményül.
Jó, jó Tanító bácsi! De mi lesz az egyforma számokkal? Azok milyen sorszámot kapnak? Hát igen, Pistike! Ez megkerülhetetlen probléma. A legegyszerűbb ha nézünk egy példát és rögtön kipróbáljuk a RANG.ÁTL-ot is, mert annak az argumentum-listája azonos a RANG.EGY-ével.
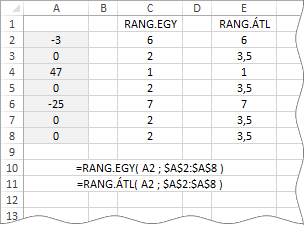
Ahogy látjuk a RANG.EGY „nem tesz” igazságot: az azonos számok a sorrendben következő pozíció-számot kapják. Az őket követő elem rangsor-pozíciója az utolsó „kiosztott” sorszám és az ismétlődések számának összege lesz. A példánkban, a rangsorban a négy nullát követő mínusz három rangsor-pozíciója: 2+4 » 6. A RANG.ÁTL függvény csak az azonos számok sorszámozásában különbözik a testvérétől. Ő is azonos pozíció számot ad az ismétlődéseknek, de nem a következőt, hanem az ismétlődések által elfoglalt rangsor-pozíciók átlagát. Másként fogalmazva, az ismétlődések pozíció száma az elfoglalt rangsor-pozíciók száma összegének és az ismétlődések számának hányadosa. Tehát: (2+3+4+5)/4 » 3,5. Az ismétlődéseket követő szám rangsor-pozíciójának kiszámítása azonos az előbb ismertetett eljárással. Szándékosan vezettem be a „pozíció szám” kifejezést, hogy a „tényleges” rangsor-pozíciót ne mossam össze a függvény által visszaadott számmal.
Nekem egyik megoldás sem tetszik, Tanító Bácsi! Olyan béna ez a szakadozott sorszámozás! Szerintem is, Pistike! Ha sorszámozás, akkor legyen benne „sor”, vagyis folyamatosság! Van egy mesterfogás, amellyel megoldhatjuk a problémát. Azt mondjuk, hogy az az ismétlődő szám, amely előrébb áll a halmazban, vagyis a tartományban, az a rangsorban is megelőzi a halmazban őt követő ismétlődést. Tehát a RANG.EGY által visszaadott értékhez hozzá kell adni, a megszámlálás függvényeinél megismert, előfordulás-számot. Magyarul, ha már volt ilyen szám a halmazban, akkor azok darabszámát hozzá kell adni a pozíció-számhoz. Igen ám, de az előfordulás-szám tartalmazza az aktuálisan vizsgált értéket is! Ezért ebből ki kell vonnunk egyet.
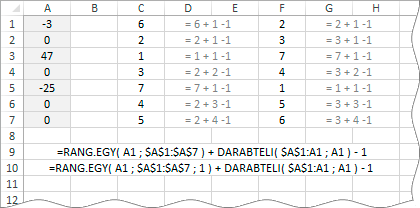
Az A oszlopban álló számok rangsora: 47, 0 (A2), 0 (A4), 0 (A6), 0 (A7), -3, -25. Már bocsánat, Tanító bácsi! De kicsit röhejes, hogy megkülönböztetjük a nullákat! Nem tök mindegy! Hááát igen, Pistike! Elég nevetséges, de ha úgy gondolunk ezekre a számokra, mint egy csoport tagjainak az egyik számszerűsíthető tulajdonságára, akkor már nem mindegy, ki az ötödik és ki a hatodik, mert biztos nem véletlenül rangsorolták ezeket az embereket…
Itt a vége, fuss el véle! Na és a SORSZÁM-mal mi lesz? Jaj, tényleg, róla teljesen megfeledkeztem! Tudod, Pistike, amikor még nem volt RANG.EGY és még RANG.ÁTL se, akkor csak a SORSZÁM volt, ami pont ugyan úgy működött mint, a RANG.EGY. De, amikor már volt RANG.EGY és RANG.ÁTL is, a SORSZÁM akkor is maradt. A kompatibilitás miatt.

 margitfalvi.arpad@gmail.com
margitfalvi.arpad@gmail.com
